Análisis de la vibración

Hay diversas variaciones en el tema CVT, en la mayoría de los autos de pasajeros las mitades de cada polea están alineadas con los extremos puntiagudos de los conos tocando. Estos forman una ranura en forma de V en la que la correa de conexión cabalga. Un lado de la polea está fijo, y el otro lado es móvil, accionado por un cilindro hidráulico. El cilindro puede aumentar o disminuir la cantidad de espacio entre los dos lados de la polea. Esto permite que la correa viaje más abajo o más a lo largo de las paredes de la polea, dependiendo de las condiciones de conducción, cambiando así la relación de "engranaje".

La naturaleza sin pasos de su diseño es la mayor ventaja del CVT para los ingenieros automotrices. Debido a ello, un CVT puede trabajar para mantener el motor en su rango de potencia óptimo, aumentando la eficiencia y el kilometraje de combustible al ofrecer un número infinito de transiciones suaves de baja a alta. Y es esta variabilidad infinita la que, según la EPA, puede aumentar la economía de combustible de un turismo en aproximadamente un 6 por ciento.

Análisis de la vibración 

Cualquier cosa vibra, y esa vibración se puede representar con el siguiente sistema (masa-resorte-amortiguador)

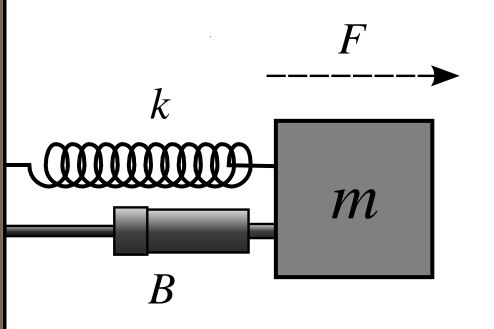
Este sistema lo podemos alterar mediante una fuerza aplicada a la masa. Las tres leyes de Newton, indican que para alterar el estado de reposo o movimiento de una masa, se tiene que aplicar una fuerza para que la masa reaccione de manera contraria pero sin alterar la magnitud a la fuerza perturbadora. Esa fuerza se calcula con la formula de F=m*a

Donde

F= Fuerza

M=Masa

a= Aceleración 

Si se quiere alterar el estado de movimiento de un objeto, se debe aplicar una velocidad o tirón en un fluido. 

Todo se puede simular con el modelo anterior visto.

Una bascula de resorte, tiene la ley de Hooke. Esta ley nos dice que la fuerza que deforma un resorte es directamente proporcional a la deformación que sufre el resorte multiplicada por una constante proporcional. Esta constante viene dada por el fabricante mediante pruebas experimentales. 

Las ligas sufren cambios en su longitud y si multiplicamos por la constante proporcional de ese elemento, nos arroja la fuerza con la que se esta deformando ese elemento. 

Todo lo antes mencionado, se reduce a estas tres ecuaciones:

1.  F=k*x   (Ley de Hooke)
2. F=C*x   (Segunda ley de Newton)
3. F=m*x   (Tercera ley de Newton)

Si multiplicamos la constante del resorte por la primera derivada del movimiento de la masa, se obtiene la fuerza con la que el amortiguador se esta desplazando. El amortiguador funciona con algún tipo de fluido. (Aire, aceite), el fluido reduce la fuerza con la que se mueve el amortiguador.

La primera derivada de la posición es la velocidad 

La segunda derivada de la posición es la aceleración 

Esto se puede aplicar en cualquier material. Por ejemplo al estirar una liga en el agua o algún otro fluido, esto se complica mas a diferencia de  que si estuviese en el aire.

 

Del sistema mostrado anteriormente, se puede decir que:

• El resorte y el punto donde se aplica la fuerza, no representa una masa para el modelo, la masa del resorte es muy inferior a la masa que se quiere desplazar.
• La masa no sufre deformación, es decir, es rígida.
• El amortiguador concentra sus efectos en el punto donde se aplica la fuerza.

Si se aplica sumatoria de fuerzas, podemos decir que:

• La fuerza en el resorte más la fuerza en el amortiguador más la fuerza que opone la masa de ser movida más la fuerza que se esta aplicando en la mas, nos debe de dar cero.

• Para el amortiguador, como se esta multiplicando por la velocidad se mide en kilogramo sobre segundo.

• Para la masa se mide en kilogramos.

El sistema mecánico rotacional, se puede aplicar un torque, el cual es solo una fuerza. 

La inercia se aplica en los motores, el motor consume mas corriente cuando se arranca el motor, esto para poder romper esa inercia. 

En los rodamientos tenemos tres tipos diferentes de fricción:

• Estática
• Viscosa
• Coulomb